In 1706 young Neidhardt, full of importance as the author of a new book on temperament, Beste und leichteste Temperatur des Monochordi, held a tuning contest with Sebastian Bach’s cousin, Johann Nikolaus Bach, in Jena. Neidhardt tuned one set of pipes by a monochord he had computed by making an arithmetical division of the syntonic comma. Therefore, although he had worked out this division to six places, it was about as accurate as the practical monochord given above. Bach tuned another set of pipes entirely by ear, and won the contest handily, for a singer found it easier to sing a chorale in Bb minor in Bach’s tuning than in Neidhardt’s.
J. Murray Barbour
Nonostante l’aspetto teorico-matematico domini incontrastato da secoli, l’accordatura è pragmaticamente legata alla capacità dell’udito umano di riconoscere gli intervalli puri e di confrontare i battimenti di intervalli non puri, purché la frequenza degli stessi battimenti non sia troppo elevata o troppo bassa.
Se da un lato i teorici si avvalevano del monocordo, in omaggio alla prassi antica, dall’altro si erano resi conto che è molto arduo valutare correttamente minuscole frazioni di semitono, come lo schisma, riportando su una corda vibrante tesa fra due capi mobili le lunghezze calcolate con complessi rapporti matematici.
Ci fu anche chi usò una canna campione, di cui era possibile modificare la lunghezza (tenendo addirittura conto della correzione di bocca).
Le speculazioni teoriche produssero frutti nel lungo periodo, mentre la prassi reale continuò con aggiustamenti empirici; le descrizioni dei procedimenti sono spesso poco chiare, insufficienti, affidate all’intuizione del lettore.
Basti citare il caso di Arnold Schlick, autore dello Spiegel der Orgelmacher und Organisten, Magonza, 1511 (edizione moderna in Monatshefte fur Musikgeschichte, 1869, p. 41 e segg.). Shohe Tanaka e Hugo Riemann hanno trasmesso l’idea errata che Schlick abbia fondato il sistema mesotonico, ma ciò non è affatto vero: le sue istruzioni sono state interpretate in almeno altri cinque diversi modi, con risultati non sovrapponibili.
Solo in epoca moderna si cominciò a contare con precisione il numero di battimenti di un intervallo nell’unità di tempo. Infatti è solo quando si conoscono il corista, l’esatta altezza delle note e la frequenza dei battimenti che è possibile replicare uno schema di accordatura.
È noto che, ad esempio, due battimenti al secondo nella regione del 4′ raddoppiano all’ottava superiore, inoltre ogni variazione di corista si ripercuote sulla frequenza dei battimenti stessi. Inutile ricordare poi che la misurazione del tempo richiede una tecnologia che maturò lentamente nel corso dell’epoca moderna.
Un ipotetico temperamento in cui tutte e 12 le quinte presentino lo stesso identico numero di battimenti non potrà dirsi regolare, per il fatto che a mano a mano che le frequenze delle note si alzano, bisognerà temperare sempre di meno l’intervallo per mantenere costante l’effetto acustico. Infatti nel temperamento equabile, che è regolare, la frequenza di battimento delle quinte aumenta proporzionalmente alla tessitura in cui sono collocate.
In questa rapida descrizione esaminerò soprattutto i sistemi che possono essere costruiti con discreta precisione avvalendosi dell’orecchio e del metronomo.
Il primo teorico europeo ad allontanarsi dall’accordatura pitagorica del monocordo cromatico fu probabilmente Bartolomeus Ramis de Pareja. [ Musica practica, Bologna, 1482; edizione moderna a cura di Johannes Wolf in Beiheft der Internationale Musikgesellschaft, 1901].
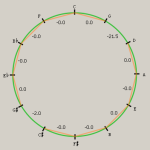
Ramis de Pareja diede specifiche indicazioni per accordare il monocordo in modo da costruire un sistema in cui le sei note A♭, E♭, B♭, F, C, G sono incatenate alla distanza di quinta pura, come nel sistema pitagorico, e le sei rimanenti note, D, A, E, B, F♯, C♯ sono anch’esse separate da quinte pure, ma scalate verso il basso di un intero comma sintonico rispetto al sistema pitagorico, così da generare quattro terze maggiori pure sulle note B♭, F, C, G. Lo schisma si scarica nella sesta diminuita C♯-A♭.
Questa nuova suddivisione fu pensata da Ramis de Pareja per il solo motivo di semplificare la costruzione del monocordo. Stando alle sue parole, il sistema pitagorico illustrato da Boezio è utile e allettante per i teorici, ma fastidioso per i cantanti e impervio.
| C | 1/1 | 0.000000 | unison, perfect prime |
| C# | 135/128 | 92.178716 | major chroma, major limma |
| D | 10/9 | 182.403712 | minor whole tone |
| Eb | 32/27 | 294.134997 | Pythagorean minor third |
| E | 5/4 | 386.313714 | major third |
| F | 4/3 | 498.044999 | perfect fourth |
| F# | 45/32 | 590.223716 | diatonic tritone |
| G | 3/2 | 701.955001 | perfect fifth |
| G# | 128/81 | 792.179997 | Pythagorean minor sixth |
| A | 5/3 | 884.358713 | major sixth, BP sixth |
| Bb | 16/9 | 996.089998 | Pythagorean minor seventh |
| B | 15/8 | 1088.268715 | classic major seventh |
| c | 2/1 | 1200.000000 | octave |
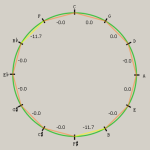
Nella biblioteca universitaria di Erlangen si conserva un manoscritto d’area tedesca risalente alla seconda metà del Quattrocento, Pro clavichordiis faciendis, che espone un metodo pratico di accordatura vicino a quello proposto da Ramis de Pareja. Inizia con la nota B, e presenta un semitono B-C che vale 16:15, la quarta B-E che vale 4:3 e la sesta minore pura B-G che vale 8:5. Una serie di quinte pure verso l’ordine dei bemolli si estende sino al G♭, cui seguono una terza maggiore pura discendente G♭-E♭♭ (5:4) e quindi una quinta pura ascendente E♭♭-B♭♭.
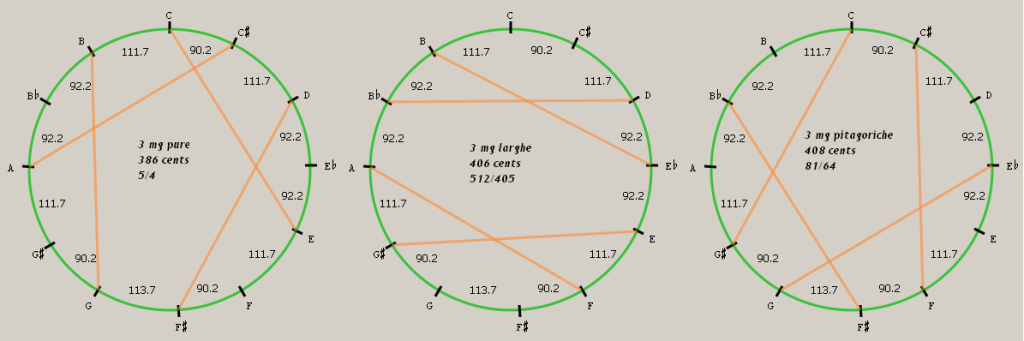
| C | 1/1 | 0.000000 | unison, perfect prime |
| D♭ | 256/243 | 90.224996 | limma, Pythagorean minor second |
| E♭♭ | 4096/3645 | 201.956281 | narrow diminished third |
| E♭ | 32/27 | 294.134997 | Pythagorean minor third |
| E | 5/4 | 386.313714 | major third |
| F | 4/3 | 498.044999 | perfect fourth |
| G♭ | 1024/729 | 588.269995 | Pythagorean diminished fifth |
| G | 3/2 | 701.955001 | perfect fifth |
| A♭ | 128/81 | 792.179997 | Pythagorean minor sixth |
| B♭♭ | 2048/1215 | 903.911282 | narrow diminished seventh |
| B♭ | 16/9 | 996.089998 | Pythagorean minor seventh |
| B | 15/8 | 1088.268715 | classic major seventh |
| c | 2/1 | 1200.000000 | octave |
Questo monocordo può essere reinterpretato tenendo conto dello schisma e dell’enarmonia, che probabilmente l’anonimo autore sottointendeva, dato che indica i vari semitoni semplicemente numerandoli: fra C e D sta il primo, fra D e E il secondo, eccetera; in questo modo J. Murray Barbour, Tuning and Temperament, a historical survey, 1951, Michigan State College Press, ottiene una seconda versione quasi equivalente:
| Nota | C | C♯ | D | E♭ | E | F | F♯ | G | A♭ | A | B♭ | B | c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cents | 0 | 92 | 204 | 294 | 386 | 498 | 590 | 702 | 794 | 906 | 996 | 1088 | 1200 |
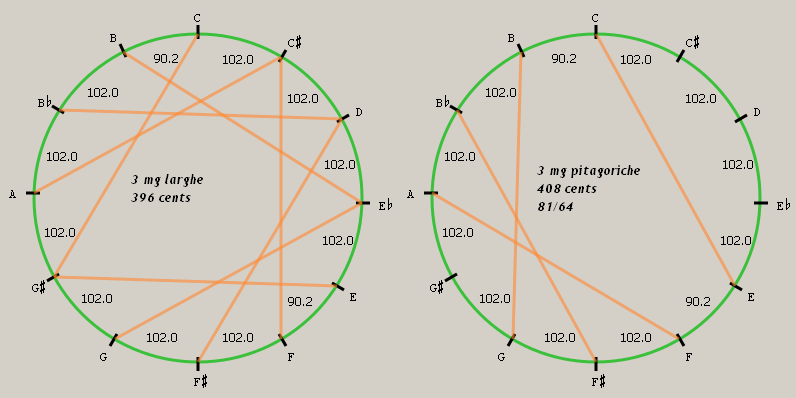
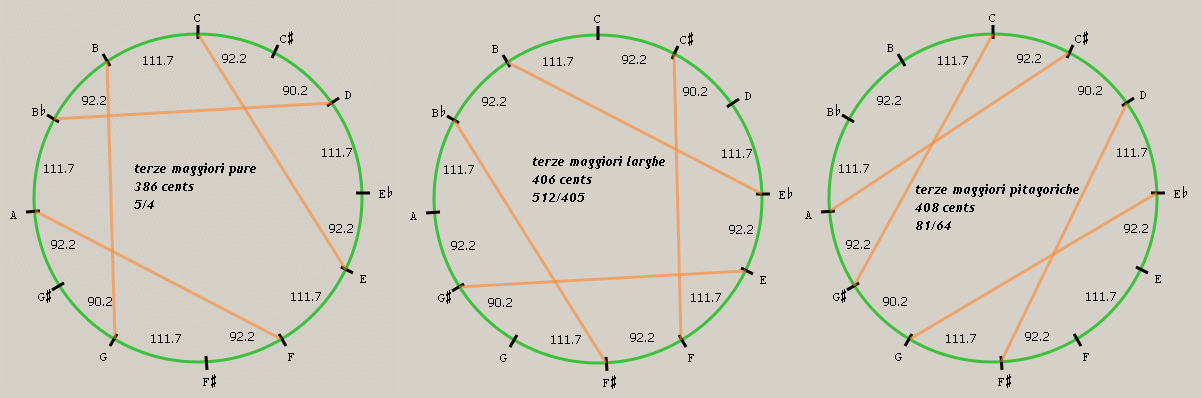
Il matematico Heinrich Schreiber, noto anche come Grammateus, pubblicò un trattato dal titolo Ayn new kunstlich Buech welches gar gewiss vnd behend lernet nach der gemainen Regel detre Grammateum oder Schreyber (Stuchs, Nürnberg 1518) in cui calcolava per via geometrica, anziché aritmetica, la lunghezza da assegnare a canne d’organo accordate secondo un sistema pitagorico modificato, in cui i toni interi diatonici sono divisi in semitoni identici per ampiezza. Jacques Lefevre d’Etaples aveva descritto un metodo analogo già nel 1496. Ciascuna alterazione produce semitoni di 102 cents sia in aumento che in diminuzione, mentre il semitono diatonico mantiene la sua naturale ampiezza di 90 cents. Spartendo il comma pitagorico in due metà di 12 cents l’una, si stringono a 690 cents le due quinte B♭-F e B-F♭. Ne derivano otto terze maggiori poco più larghe del valore naturale, 396 cents. Purtroppo esse sono disposte lontano dalle tonalità più usate, tre delle quali (Fa, Do e Sol maggiore) hanno la terza pitagorica, che si digerisce a stento. Le quinte invece sono pure, tranne i due lupi che non sono però mostruosi. In epoca moderna il sistema ha avuto qualche fortuna con la letteratura virginalistica elisabettiana (Fitzwilliam Virginal Book).
| C | 1/1 | 0.000000 | unison, perfect prime |
| C♯ | – | 101.955000 | |
| D | 9/8 | 203.910002 | major whole tone |
| E♭ | – | 305.865000 | |
| E | 81/64 | 407.820003 | Pythagorean major third |
| F | 4/3 | 498.044999 | perfect fourth |
| F♯ | – | 600.000000 | |
| G | 3/2 | 701.955001 | perfect fifth |
| A♭ | – | 803.910000 | |
| A | 27/16 | 905.865003 | Pythagorean major sixth |
| B♭ | – | 1007.820000 | |
| B | 243/128 | 1109.775004 | Pythagorean major seventh |
| c | 2/1 | 1200.000000 | octave |