Il sistema mesotonico a 1/3 di comma
La scala diatonica presenta sette gradi ricavati concatenando sei quinte: FA-DO-SOL-RE-LA-MI-SI. Poste in successione ascendente le note sono separate da intervalli di tono (do-re, re-mi, fa-sol, sol-la, la-si) e semitono diatonico (mi-fa, si-do). Se le quinte sono pure, per gli intervalli di tono vale il rapporto 9:8, ossia 204¢; per gli intervalli di semitono diatonico vale il rapporto 256:243, circa 90¢. Si nota subito che il semitono diatonico non equivale a mezzo tono. Se calcoliamo la differenza tra tono e semitono diatonico (204-90=114¢) otteniamo un altro intervallo chiamato apotome. Esso è più ampio del semitono suddetto (limma usando la terminologia pitagorica) di un comma pitagorico, cioè 24¢.
Proseguendo nella concatenazione di quinte possiamo espandere la scala al cosiddetto genere cromatico: se aggiungiamo altre sei quinte ascendendo dalla nota SI, cui eravamo arrivati, otteniamo i semitoni cromatici nell’ordine dei diesis (FA♯-DO♯-SOL♯-RE♯-LA♯-MI♯); se aggiungiamo altre sei quinte discendendo dalla nota di partenza FA, troviamo i semitoni cromatici nell’ordine dei bemolli (SI♭-MI♭-LA♭-RE♭-SOL♭-DO♭). Nel sistema pitagorico il semitono cromatico coincide con l’apotome.
Così facendo abbiamo generato 19 note e collegato fra loro 18 quinte. Tra MI♯ e DO♭ esiste un intervallo di sesta più che diminuita che ha l’ampiezza di 565 ¢ e dunque appare all’ascolto come una sorta di tritono. L’intervallo complementare DO♭-MI♯ è formalmente una terza più che aumentata, e avendo l’ampiezza di 635¢ suona come una quinta strettissima.
Se accettiamo di compromettere la purezza delle quinte, stringendole tutte omogeneamente, in modo da dividere l’ottava in 19 parti uguali, riusciamo ad abbassare il MI♯ e alzare il DO♭ sino a creare fra loro un intervallo che suona come una quinta temperata uguale alle altre, pur rimanendo formalmente una sesta più che diminuita. In questo nuovo assetto delle note se dal MI♯ saliamo di una quinta temperata, raggiungiamo il SI♯ che coincide con il DO♭. Analogamente se da DO♭ scendiamo di quinta temperata, raggiungiamo il FA♭, che si sovrappone al MI♯. È così possibile considerare MI♯ come FA♭ per avere la quinta giusta FA♭-DO♭ oppure chiamare SI♯ il DO♭ per indicare la quinta giusta MI♯-SI♯. Pertanto abbiamo temperato 19 quinte.
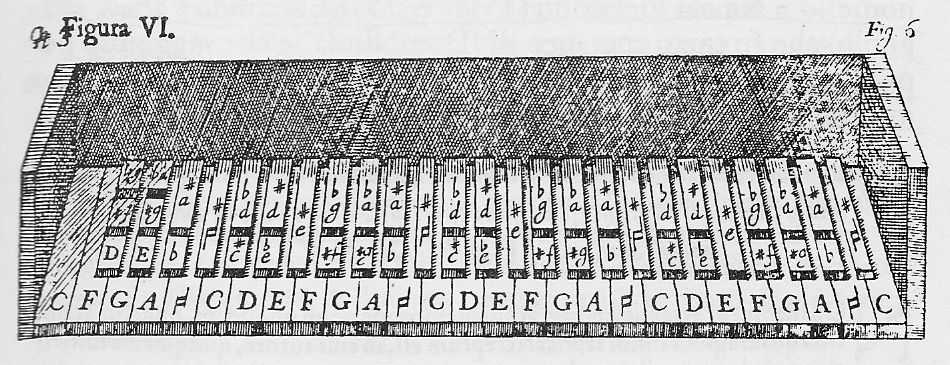
Ebbene, immaginiamo una tastiera le cui ottave presentino 19 tasti, come quella illustrata da J. B. Samber, Manuductio ad organum, Salisburgo, 1704, Parte I, p. 103:
Concatenando 19 quinte pure copriamo l’estensione di 11 ottave, con un eccesso in cents pari a (701.955 × 19) – (1200 × 11), cioè 13337.145 – 13200 = 137.145.
La quantità di cui si deve temperare ciascuna quinta per ottenere la suddivisione dell’ottava in 19 parti uguali è dunque 137.145¢ ÷ 19 = 7.218¢. Seguendo questa via, creiamo un sistema equabile i cui gradi hanno frequenze in rapporto costante di 1 : 19√2, cioè un intervallo di 63.157895¢.
Il valore trovato è prossimo a 1/3 di comma sintonico, che esattamente vale 7.169¢. È allora possibile creare anche un sistema mesotonico molto simile al precedente, ma più semplice da realizzare, perché, temperando le quinte di 1/3 di comma sintonico, si generano terze minori pure.
Rispetto al sistema equabile (ET19) la successione delle quinte nel sistema mesotonico presenta uno scarto minuscolo (circa 1 cent), che trascuriamo per poter chiudere il circolo, ma che deve però essere seriamente preso in considerazione al momento dell’accordatura. Infatti possiamo intonare pure solo le terze minori che compaiono usando la nomenclatura reale: quelle fittizie, ottenute per enarmonia, non possono essere usate per l’intonazione, perché a rigore sono delle seconde aumentate, consonanti quasi fossero terze minori (per esempio fa – sol♯). Dunque nel sistema sono possibili tre distinte catene di terze minori:
- si♯ – re♯ – fa♯ – la – do – mi♭ – sol♭,
- la♯ – do♯ – mi – sol – si♭ – re♭,
- mi♯ – sol♯ – si – re – fa – la♭.
Invece nel sistema equabile (ET19) compare una catena di terze minori virtualmente chiusa: cominciando da do, ad esempio, possiamo salire attraverso mi♭, sol♭, si♭♭ ≈ la♯, do♯, mi, sol, si♭, re♭, fa♭ ≈ mi♯, sol♯, si, re, fa, la♭, do♭, mi♭♭ ≈ re♯, fa♯, la, do. Questi intervalli sono tra loro uguali in ampiezza, 315.789¢, all’orecchio praticamente indistinguibili dall’intervallo naturale 315.641¢. Pertanto entrambi i sistemi si possono ritenere circolari. Il meccanismo dell’enarmonia è praticabile, e con 19 tasti per ottava è ricchissimo di sfumature. Nella seguente tabella gli effettivi nomi di nota e i gradi della scala sono dati nelle prime tre colonne a sinistra. Nelle colonne a destra sono esposti i valori in cents per il sistema equabile, che non usa frazioni di comma sintonico e quindi non produce terze minori rigorosamente pure.
| mesotonico 1/3 | equabile (ET19) | ||||
|---|---|---|---|---|---|
| nota | cents | gradi | cents | gradi | equivalenza |
| do | 0.000 | 63.504 | 0.000 | 63.158 | |
| do♯ | 63.504 | 62.565 | 63.158 | 63.158 | |
| re♭ | 126.069 | 63.504 | 126.316 | 63.158 | |
| re | 189.572 | 63.504 | 189.474 | 63.158 | |
| re♯ | 253.076 | 62.565 | 252.632 | 63.158 | |
| mi♭ | 315.641 | 63.504 | 315.789 | 63.158 | |
| mi | 379.145 | 63.504 | 378.947 | 63.158 | |
| fa♭ | 441.710 | 0.939 | 442.105 | 0.000 | fa♭=mi♯ mesotonico 442,649 |
| mi♯ | 442.649 | 62.565 | 442.105 | 63.158 | |
| fa | 505.214 | 63.504 | 505.263 | 63.158 | |
| fa♯ | 568.717 | 62.565 | 568.421 | 63.158 | |
| sol♭ | 631.283 | 63.504 | 631.579 | 63.158 | |
| sol | 694.786 | 63.504 | 694.737 | 63.158 | |
| sol♯ | 758.290 | 62.565 | 757.895 | 63.158 | |
| la♭ | 820.855 | 63.504 | 821.053 | 63.158 | |
| la | 884.359 | 63.504 | 884.211 | 63.158 | |
| la♯ | 947.862 | 62.565 | 947.368 | 63.158 | |
| si♭ | 1010.428 | 63.504 | 1010.526 | 63.158 | |
| si | 1073.931 | 62.565 | 1073.684 | 63.158 | |
| do♭ | 1136.496 | 0.939 | 1136.842 | 0.000 | do♭=si♯ mesotonico 1136.496 |
| si♯ | 1137.435 | 62.565 | 1136.842 | 63.158 | |
| do | 1200.000 | 1200.000 | |||
La divisione dell’ottava in più di dodici parti fu praticata nel Rinascimento attraverso la costruzione di strumenti con tastiere “ampliate”, con tasti spezzati o disposti su più ordini.
Guillaume Costelay intorno alla metà del XVI secolo compose una chanson che richiede un cembalo microtonale con l’ottava divisa in diciannove note.
Francisco de Salinas (De musica libri VII, Salamanca, 1577, p. 143) fu il primo teorico a descrivere il sistema in oggetto. Egli propose di dividere il tono in tre parti uguali, attribuendone due al semitono diatonico e una a quello cromatico, ottenendo una gamma costituita da 19 intervalli.
La realizzazione illustrata da Salinas al monocordo richiede l’accordatura concatenata di sette terze minori pure: B♯-D♯-F♯-A-C-E♭-G♭; quindi è necessario ricorrere al mesolabio per trovare i due medi proporzionali nel tritono C-F♯, fissando così la lunghezza delle corde D e E. Infine bisogna accordare le rimanenti catene di terze minori pure sopra e sotto le note D e E, per trovare F-A♭, E♯-G♯-B, G-B♭-D♭, C♯-A♯.
Patrizio Barbieri illustra i metodi impiegati anticamente per il calcolo delle proporzioni musicali nell’articolo Il mesolabio e il compasso di proporzione: le applicazioni musicali di due strumenti matematici (1558-1675) pubblicato nel volume Musica, scienza e idee nella Serenissima durante il Seicento, 1996, Fondazione Levi – Venezia.
Per realizzare il sistema di temperamento sulle normali tastiere con divisione dell’ottava in 12 parti, eliminiamo le note che non sono abitualmente praticate nella letteratura tastieristica antica, cioè re♭, sol♭, la♭, re♯, la♯, oltre a mi♯ e do♭, ottenendo la seguente disposizione:
| Nota | Rapporto | Intervallo | Scala di 12 gradi | Scala di 19 gradi |
| C | 1/1 | unison, perfect prime | 0.000 | 0.000 |
| C♯ | 63.504 | 63.504 | ||
| D♭ | 126.069 | |||
| D | 189.572 | 189.572 | ||
| D♯ | 125/108 | semi-augmented whole tone | 253.076 | |
| E♭ | 6/5 | minor third | 315.641 | 315.641 |
| E | 379.145 | 379.145 | ||
| E♯ | 442.649 | |||
| F | 505.214 | 505.214 | ||
| F♯ | 25/18 | classic augmented fourth | 568.717 | 568.717 |
| G♭ | 36/25 | classic diminished fifth | 631.283 | |
| G | 694.786 | 694.786 | ||
| G♯ | 758.290 | 758.290 | ||
| A♭ | 820.855 | |||
| A | 5/3 | major sixth, BP sixth | 884.359 | 884.359 |
| A♯ | 947.862 | |||
| B♭ | 1010.428 | 1010.428 | ||
| B | 1073.931 | 1073.931 | ||
| B♯ | 1136.496 | |||
| c | 2/1 | octave | 1200.000 | 1200.000 |
La procedura per accordare i dodici gradi della scala è molto semplice e si avvale di un metronomo per contare la frequenza dei battimenti e per confrontare gli intervalli-pilota.
Si può iniziare dal La corista, sul quale si intonano la terza minore pura La2-Do3 e il suo rivolto Do2-La2. Pura deve essere accordata la terza minore Fa♯2-La2, come anche Do2-Mi♭2.
Seguendo la tabella sottostante, si pone il metronomo a 65 battiti al minuto e si scandiscono terzine, che costituiscono il modello per contare il numero di battimenti della quinta Do2-Sol2: essa deve essere stretta intervenendo sulla nota Sol. Mantenendo la pulsazione del metronomo si accorda quindi il Mi2, scendendo dal La: ora si devono scandire quintine, che dànno la velocità della quarta Mi2-La2. La terza maggiore Do2-Mi2 deve avere lo stesso numero di battimenti della quarta Mi2-La2. Se si è operato con accuratezza, la terza minore Mi2-Sol2 deve riuscire pura.
Sul Sol2 si intona il Si♭2 e sul Mi2 si accorda il Do♯2 in modo da avere terze minori pure.
Si tratta ora di replicare la procedura illustrata, aggiungendo le due note Re2 e Si2. Si accorda quindi il Re2, cosicché la quinta Re2-La2 sia stretta e inoltre il Si2 è intonato a formare sesta maggiore pura col Re2: la quarta risultante Fa♯2-Si2 rispetta la proporzione ritmica indicata sopra, ma con il metronomo impostato su 73 battiti al minuto, cioè quintine per la quarta Fa♯2-Si2 e per la terza maggiore Re2-Fa♯2, e terzine per la quinta Re1-La2.
La quinta Mi2-Si2 è già formata, e dovrebbe scandire terzine con il metronomo impostato a 81 battiti al minuto: non rimane che accordare il Sol♯2 terza minore pura sotto il Si2 ed il Fa2 terza minore pura sopra il Re2.
Nelle triadi minori in primo rivolto si deve verificare sempre l’uguaglianza del numero di battimenti di terza maggiore e quarta. Un ulteriore controllo si può fare confrontando la quarta e la quinta sopra una medesima nota: a parità di metronomo la prima scandisce quartine e la seconda terzine.
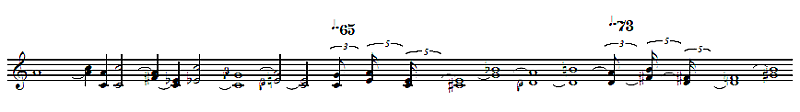
Corista A3: 440 Hz con il Do3 a 264.00 Hz
La frequenza di battimenti in cicli/minuto è ottenuta con il metronomo impostato per scandire in una singola pulsazione i gruppetti indicati.
| Quinta | ratio 3:2 | |||||
|---|---|---|---|---|---|---|
| nota | Hertz | |||||
| C | 264.000000 | 196.366 | 98.183 | 65.455 | 49.091 | 39.273 |
| C♯ | 273.863623 | 203.702 | 101.851 | 67.901 | 50.926 | 40.740 |
| D | 294.550499 | 219.090 | 109.545 | 73.030 | 54.772 | 43.818 |
| E♭ | 316.800000 | 235.639 | 117.820 | 78.546 | 58.910 | 47.128 |
| E | 328.636348 | 244.443 | 122.221 | 81.481 | 61.111 | 48.889 |
| F | 353.460597 | 262.907 | 131.454 | 87.636 | 65.727 | 52.581 |
| F♯ | 366.666667 | 272.731 | 136.365 | 90.910 | 68.183 | 54.546 |
| G | 394.363618 | 293.332 | 146.666 | 97.777 | 73.333 | 58.666 |
| G♯ | 409.097914 | 2394.376 | 1197.188 | 798.125 | 598.594 | 478.875 |
| A | 440.000000 | 327.276 | 163.638 | 109.092 | 81.819 | 65.455 |
| B♭ | 473.236340 | 351.998 | 175.999 | 117.333 | 87.999 | 70.400 |
| B | 490.917497 | 365.149 | 182.575 | 121.716 | 91.287 | 73.030 |
| c | 528.000000 | 392.732 | 196.366 | 130.911 | 98.183 | 78.546 |
| Quarta | ratio 4:3 | |||||
|---|---|---|---|---|---|---|
| nota | Hertz | |||||
| C | 264.000000 | 262.907 | 131.454 | 87.636 | 65.727 | 52.581 |
| C♯ | 273.863623 | 272.731 | 136.365 | 90.910 | 68.183 | 54.546 |
| D | 294.550499 | 293.332 | 146.666 | 97.777 | 73.333 | 58.666 |
| E♭ | 316.800000 | 2394.376 | 1197.188 | 798.125 | 598.594 | 478.875 |
| E | 328.636348 | 327.276 | 163.638 | 109.092 | 81.819 | 65.455 |
| F | 353.460597 | 351.998 | 175.999 | 117.333 | 87.999 | 70.400 |
| F♯ | 366.666667 | 365.149 | 182.575 | 121.716 | 91.287 | 73.030 |
| G | 394.363618 | 392.732 | 196.366 | 130.911 | 98.183 | 78.546 |
| G♯ | 409.097914 | 407.405 | 203.702 | 135.802 | 101.851 | 81.481 |
| A | 440.000000 | 438.180 | 219.090 | 146.060 | 109.545 | 87.636 |
| B♭ | 473.236340 | 471.278 | 235.639 | 157.093 | 117.820 | 94.256 |
| B | 490.917497 | 488.886 | 244.443 | 162.962 | 122.221 | 97.777 |
| c | 528.000000 | 525.815 | 262.907 | 175.272 | 131.454 | 105.163 |
| Terza Magg. | ratio 5:4 | |||||
|---|---|---|---|---|---|---|
| nota | Hertz | |||||
| C | 264.000000 | 327.276 | 163.638 | 109.092 | 81.819 | 65.455 |
| C♯ | 273.863623 | 2671.456 | 1335.728 | 890.485 | 667.864 | 534.291 |
| D | 294.550499 | 365.150 | 182.575 | 121.717 | 91.287 | 73.030 |
| E♭ | 316.800000 | 392.732 | 196.366 | 130.911 | 98.183 | 78.546 |
| E | 328.636348 | 407.405 | 203.703 | 135.802 | 101.851 | 81.481 |
| F | 353.460597 | 438.179 | 219.090 | 146.060 | 109.545 | 87.636 |
| F♯ | 366.666667 | 3576.722 | 1788.361 | 1192.241 | 894.180 | 715.344 |
| G | 394.363618 | 488.886 | 244.443 | 162.962 | 122.222 | 97.777 |
| G♯ | 409.097914 | 3990.626 | 1995.313 | 1330.209 | 997.656 | 798.125 |
| A | 440.000000 | 545.461 | 272.731 | 181.820 | 136.365 | 109.092 |
| B♭ | 473.236340 | 586.663 | 293.331 | 195.554 | 146.666 | 117.333 |
| B | 490.917497 | 4788.751 | 2394.375 | 1596.250 | 1197.188 | 957.750 |
| c | 528.000000 | 654.553 | 327.276 | 218.184 | 163.638 | 130.911 |
È utile confrontare lo scostamento in cents dalle note del sistema equabile. Facendo pari a 0¢ la nota DO oppure la nota LA, otteniamo i seguenti valori con cui settare gli accordatori digitali:
| riferimento | DO | DO♯ | RE | MI♭ | MI | FA | FA♯ | SOL | SOL♯ | LA | SI♭ | SI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DO | 0 | -36.5 | -10.5 | 15.5 | -21 | 5 | -31 | -5 | -41.5 | -15.5 | 10.5 | -26 |
| LA | 15.5 | -21 | 5 | 31 | -5 | 21 | -15.5 | 10.5 | -26 | 0 | 26 | -10.5 |
Anche se notevolmente impoverito quando l’ottava è divisa solo in dodici parti, il sistema è ancora apprezzabile. Le quinte non sono troppo deteriorate, e le terze maggiori strette conservano una certa eufonia.
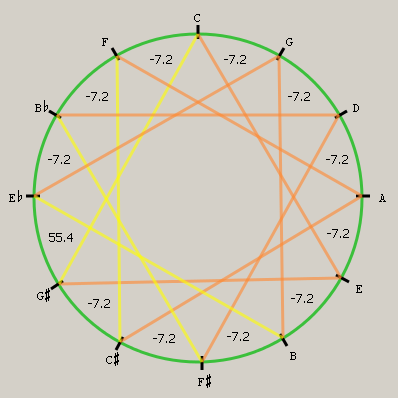
- Il lupo compare fra gli estremi del circolo, cioè fra G♯ e E♭ con un eccesso di ben 55.4 ¢, mentre le quinte sono strette di 7.2 ¢ cioè valgono 695 ¢.
- Si notano sei tritoni di giusta intonazione nel rapporto 25:18, dato dalla differenza tra sesta maggiore e terza minore (5/3 × 5/6 = 25/18) pari a 569 ¢
- Nove terze minori sono pure, valgono 316 ¢ (rapporto 6:5), tre seconde aumentate valgono 253 ¢ (rapporto 125:108) e sono F-G♯, B♭-C♯ e E♭-F♯.
- Otto terze maggiori sono strette di 1/3 di comma sintonico e misurano 379 ¢; curiosamente le quattro quarte diminuite (G♯-C, C♯-F, F♯-B♭, B-E♭) e la terza aumentata (E♭-G♯) sono quasi equivalenti (441.7 ¢ e 442.6 ¢ rispettivamente): in parole povere le “terze” non praticabili sono pressochè identiche al lupo.
- Per definizione, dieci intervalli di tono e dieci settime minori sono omogenei: i primi valgono 189.5 ¢ e le seconde 1010.5 ¢; si nota che il tono divide esattamente a metà la terza maggiore.
- Il semitono cromatico è molto piccolo, 63.5 ¢, mentre il semitono diatonico è grande il doppio, 126 ¢.