Andreas Werckmeister (1645 – 1706) fu organista e teorico musicale tedesco; è noto agli organisti per il trattato Erweiterte und verbesserte Orgelprobe, Quedlinburg, 1698 (e Augsburg, Johann Jakob Lotter, 1783). Fu autore di alcuni diffusi sistemi di temperamento della scala.
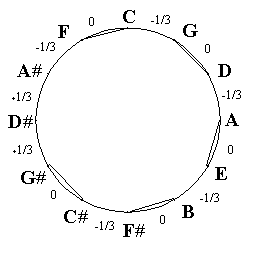
Il comma pitagorico – non quello sintonico – anziché in quattro parti uguali, come invece avviene in altri sistemi, è ripartito in tre, con la conseguenza che nove quinte su dodici risultano pure. L’effetto dei battimenti è ben sensibile, essendo le quinte temperate più strette che nel sistema equabile moderno. Questi sono lo schema degli intervalli e il relativo quadro.
Quinte Terze
Eb +0.36 64
Bb -0.36 0.27
F 0 0.27
C -0.36 27
G 0 27
D -0.36 27
A 0 27
E -0.36 27
B 0 1
F# -0.36 136
C# 0 136
G# +0.36 136
La difficoltà maggiore nella realizzazione di questo temperamento sta in due ragioni: la serie di quinte pure è interrotta e poi ripresa a distanza; si richiede di temperare di un terzo di comma pitagorico una serie di quinte separate alcune calanti e altre crescenti. Per risolvere il problema si può agire semplificandolo in più momenti:
- Si procede accordando pura la quinta C-G e la serie di otto quinte discendenti da C a E attraverso F, Bb, Eb, G#, C#, F# e B; in questo modo rimangono contigue le tre quinte G-D, D-A, A-E che saranno oggetto della successiva operazione.
- Si temperano le tre quinte suddette, G-D, D-A, A-E, in modo da renderle ugualmente strette di 1/3 di comma pitagorico.
- Si deve ora rendere pura la quinta G-D, abbassando il G e stringendo di conseguenza la quinta C-G
- Ora è la volta della quinta A-E che va resa pura, alzando la nota E e conseguentemente stringendo la quinta E-B esattamente di 1/3 di comma pitagorico.
- Si tratta ora di allargare la quinta Eb-Bb, intervenendo sul Bb e stringendo Bb-F sino a renderla uguale alla contigua C-G. Si può controllare che le due quinte Eb-Bb e D-A, che sono alla distanza di un semitono, battano ugualmente, una però crescente e l’altra calante rispettivamente.
- Abbassare il C# stringendo l’intervallo F#-C# sino a renderlo uguale per battimenti a E-B contiguo: così facendo, si allarga la quinta C#-G# di 1/3 di comma pitagorico.
- L’ultimo passo consiste nello spostamento del temperamento di 1/3 di comma dall’intervallo C#-G# a G#-Eb, per mezzo del G#, in modo da rendere nuovamente pura la quinta C#-G#.
Se alla conclusione delle operazioni si è ancora lucidi, si possono verificare tutti i passi compiuti, in modo da saggiare la qualità degli intervalli temperati e delle terze risultanti. Il sistema presentato non è facile da realizzare tagliando le canne in tondo e partendo dal Do come di consueto: la soluzione più comoda è ricorrere all’accordatore elettronico…
Nella tabella seguente si indicano in cents i valori delle note di un’ottava, fatto pari a zero il Do, che è solitamente il punto iniziale dell’accordatura. Se lo scostamento dal valore della quinta giusta (701,955 cents) o della terza maggiore (386,314 cents) o della terza minore (315,641 cents) è positivo, l’intervallo è largo; altrimenti è stretto. Maggiore è lo scostamento e più frequenti sono i battimenti.
Nota Cents Quinta Scostamento C 0,000 C-G 694,135 -7,820 C# 82,406 C#-G# 701,955 0,000 D 196,090 D-A 694,135 -7,820 Eb 294,135 Eb-Bb 709,775 7,820 E 392,180 E-B 694,135 -7,820 F 498,045 F-C 701,955 0,000 F# 588,270 F#-C# 694,136 -7,819 G 694,135 G-D 701,955 0,000 G# 784,361 G#-D# 709,774 7,819 A 890,225 A-E 701,955 0,000 Bb 1003,910 Bb-F 694,135 -7,820 B 1086,315 B-F# 701,955 0,000 Terza magg. Scost. Terza min. Scost. C-E 392,180 5,866 C-Eb 294,135 -21,506 Db-F 415,639 29,325 C#-E 309,774 -5,867 D-F# 392,180 5,866 D-F 301,955 -13,686 Eb-G 400,000 13,686 D#-F# 294,135 -21,506 E-G# 392,181 5,867 E-G 301,955 -13,686 F-A 392,180 5,866 F-Ab 286,316 -29,325 F#-A# 415,640 29,326 F#-A 301,955 -13,686 G-B 392,180 5,866 G-Bb 309,775 -5,866 Ab-C 415,639 29,325 Ab-C 301,954 -13,687 A-C# 392,181 5,867 A-C 309,775 -5,866 Bb-D 392,180 5,866 Bb-Db 278,496 -37,145 B-D# 407,820 21,506 B-D# 309,775 -5,866