Teoria dell’accordatura

Il cent

Anziché operare sulle frequenze, si può adottare un’unità di misura dell’ampiezza di un intervallo, che consente di semplificare i calcoli riducendoli di grado: il cent.

Nel 1885 l’inglese Alexander John Ellis introdusse il cent ricorrendo ai logaritmi delle frequenze. Il motivo di questa apparente complicazione sta nel fatto che le proprietà dei logaritmi consentono di trasformare prodotti in somme, rapporti in differenze, elevamenti a potenza in moltiplicazioni e radicali in divisioni.

Queste sono le proprietà dei logaritmi: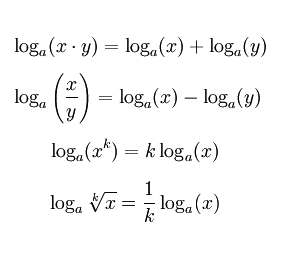

dove a, x e y sono numeri reali positivi, con a diverso da 1.

Così se per esempio vogliamo calcolare l’intervallo fra due note di 300 Hz e 240Hz possiamo ricorrere alla frazione:

300/240 = 5/4 = 0.09691

oppure alla sottrazione, giacché:

log(300/240) = log300 – log240 = 0.09691

Poniamo che l’intervallo di 1 cent sia pari alla 1200^a parte dell’ottava: è sufficientemente piccolo da consentirci di misurare con precisione tutti gli intervalli che l’orecchio umano è in grado di distinguere. Con questo accorgimento siamo in grado di rappresentare i dodici semitoni contenuti nell’ottava del temperamento equabile: se l’ottava è pari a 1200 cents e i semitoni hanno tutti la medesima ampiezza, allora un semitono vale 100 cents, un tono vale 200 cents, una quinta vale 700 cents, e così via.

Per “dividere” l’ottava in 1200 parti uguali dobbiamo estrarre la radice 1200^a del rapporto 2 a 1, ottenendo 1.00057779. Questo è il coefficiente per cui dobbiamo moltiplicare una data frequenza per ottenere il suono che si pone all’intervallo di 1 cent da essa. Ad esempio, prendiamo come riferimento il suono di frequenza 261.6 Hz (il Do dell’ottava centrale del pianoforte accordato con il sistema equabile). Per ottenere la frequenza del Do crescente di 1 cent si moltiplicherà:

261.6 × 1.00057779 = 261.7511

Altro esempio: il Sol del temperamento equabile sta una quinta “appena stretta” sopra il Do, per la precisione forma con esso un intervallo di 700 cents: la sua frequenza vale dunque:

261.6 × 2^700/1200 = 391.96 Hz

I logaritmi sono facilmente ottenuti con una calcolatrice scientifica, oppure consultando le apposite tavole logaritmiche. Però queste sono solitamente calcolate in base 10, mentre Ellis usava logaritmi in base 2. Perciò per esprimere in cents un qualsiasi rapporto tra due frequenze si deve ricorrere alla conversione di base, ossia:

cents = (1200 / log₁₀2) × log₁₀(F₂/F₁) = 3986.313715 × log₁₀(F₂/F₁)

Quindi, ritornando all’esempio precedente, la misura in cents dell’intervallo fra le frequenze di 300 Hz e 240 Hz, ossia di due suoni in rapporto di 5 a 4, è data da 3986.313715 × 0.09691 = 386.3137. Questa è la misura in cents dell’intervallo di terza maggiore pura.

Per maggior chiarezza, un intervallo I misurato in cents sta all’ottava (pari a 1200 cents) come il rapporto delle frequenze F₂/F₁ dell’intervallo sta al rapporto di ottava che vale 2. Espressa in termini matematici la proporzione è:

I / 1200 = log(F₂/F₁) / log2 da cui I = 3986.313715 × log(F₂/F₁)

Così ancora si calcola che una quinta pura (rapporto 3 a 2) vale:

3986.313715 × (log3/2) ossia 3986.313715 × (log3 – log2)

Quindi:

3986.313715 × 0,176091 = 701,955 cents

Un qualsiasi intervallo I misurato in cents si trova analogamente fra suoni le cui frequenze sono in questo rapporto:

F₂/F₁ = 10^{(log2/1200)·I} ossia F₂/F₁ = 10^{0.0002508583297·I}

Infatti, dato l’intervallo di 386.3137 cents, calcoliamo che il rapporto fra i suoni è pari a:

10^{0.0002508583297×386.3137} = 10^0.09691 = 1.25 ossia 5/4