Metodo geometrico per il calcolo della lunghezza di lastra secondo le proporzioni pitagoriche
Come s’è detto, il calcolo della lunghezza della lastra di una canna era anticamente eseguito sostanzialmente rispettando i rapporti classici della scala pitagorica, con qualche scostamento già a partire dal secolo XVII, per aderire meglio ai criteri del temperamento: è noto infatti che il circolo delle quinte pure non chiude l’ottava e che la suddivisione in semitoni ottenuta usando ripetutamente i due rapporti complementari di quinta (2/3) e quarta (3/4) giuste è leggermente sfasata rispetto a quella prevista dai vari sistemi temperati. Gli scostamenti sono irrilevanti al fine della costruzione delle canne, le cui lastre sarebbero comunque tagliate un po’ più lunghe del dovuto per consentire l’accordatura in tondo. Inoltre, pur essendo consapevoli della necessità di correggere questi valori teorici sottraendo una precisa quantità, definita correzione di bocca, tuttavia sia i teorici che gli organari la trascuravano in fase di progettazione.
Poiché si calcolano le lunghezze d’onda, non le frequenze, si debbono invertire le frazioni per cui moltiplicare l’unità di base. Quindi se la frequenza dell’ottava è pari al doppio di quella dell’unisono, allora la sua lunghezza d’onda è pari a un mezzo; se la quinta è data dal rapporto 3/2 allora la lunghezza della canna che emette la quinta è pari a 2/3 della lunghezza della canna di riferimento.
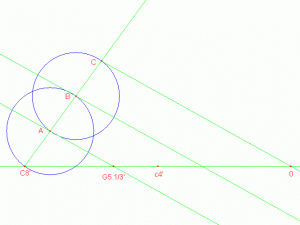Alcune proporzioni sono sempre state ritenute inviolabili: ottava e quinta giusta. I rimanenti intervalli invece erano ottenuti con diversi metodi e lievi scostamenti dalla scala pitagorica, come già si è detto.Perciò, stabilita convenzionalmente la lunghezza della lastra della canna maggiore in funzione del corista, si disegna un segmento pari a questa lunghezza, col compasso la si divide a metà, ottenendo la lunghezza dell’ottava. La quinta è ottenuta dividendo in tre parti il segmento dato e prendendone due. Divisione e moltiplicazione si ottengono con riga e compasso e sfruttando il teorema di Talete.
Molti teorici seguono le proporzioni pitagoriche anche per la quarta giusta pari a 3/4: l’ottava è presa tre volte e il segmento risultante è diviso in quattro parti oppure, trovata la lunghezza della XV, si divide in tre il segmento che ha per estremi il C8′ e il c2′.Concordano in molti anche sul rapporto 8/9 per la seconda maggiore, mentre risultano comprensibilmente meno omogenee le frazioni usate per ottenere terza maggiore e minore e loro rivolti, per le citate implicazioni con i sistemi d’accordatura (ratio pitagorica 64/81, ratio naturale 5/4).
Un metodo assai pratico, che considera irrilevanti i piccoli scostamenti dalle proporzioni pitagoriche, è quello descritto da J. van Heurn in De Orgelmaaker, un articolo comparso nella Vollendige beschrijving van alle Konsten, ambachten, handwerken… Volume 19-21, 1804/1805. Questo autore, dopo aver trovato la quinta con la solita proporzione 2/3, propone di suddividere in sette parti il segmento a sinistra e in cinque parti quello a destra, trovando così i semitoni intermedi.
Dom Bédos de Celles, L’art du facteur d’orgues, Parigi 1766-78, descrive nel primo tomo dell’opera come si divide l’ottava secondo il circolo delle quinte: adotta pragmaticamente il sistema pitagorico, dimostrando che per tagliare le lastre non riteneva necessario rispettare fedelmente il sistema d’accordatura: in effetti gli scostamenti non sono tali da pregiudicare il risultato. Egli indica come operare partendo dalla prima ottava, come estendere la suddivisione all’intero ambito del registro, e dà le lunghezze di un 4′ misurate in piedi, pollici, linee e punti (un punto vale 1/12 di linea cioè 0,188 mm). Nella seguente tabella si riportano questi valori.
| · | intervallo | nota | ratio | piedi | pollici | linee | punti | mm |
|---|---|---|---|---|---|---|---|---|
| Do | è l’unisono dato | Do | 100 | 4 | 0 | 0 | 0 | 1300 |
| 3/4 di Do | quarta giusta | Fa | 75 | 3 | 0 | 0 | 0 | 975 |
| 2/3 di Do | quinta giusta | Sol | 66,667 | 2 | 8 | 0 | 0 | 866,8 |
| 4/3 di Sol | quarta discendente, seconda maggiore sul Do | Re | 88,889 | 3 | 6 | 8 | 0 | 1155,68 |
| 2/3 di Re | quinta sopra, sesta maggiore sul Do | La | 59,259 | 2 | 4 | 5 | 4 | 770,4533 |
| 4/3 di La | quarta inferiore, terza maggiore sul Do | Mi | 79,012 | 3 | 1 | 11 | 1 | 1027,148 |
| 2/3 di Mi | quinta sopra, settima maggiore sul Do | Si | 52,675 | 2 | 1 | 3 | 4 | 684,6333 |
| 3/4 di Fa | quarta sopra, settima minore sul Do | Si♭ | 56,25 | 2 | 3 | 0 | 0 | 731,3 |
| 3/2 di Si♭ | quinta discendente, terza minore sul Do | Mi♭ | 84,375 | 3 | 4 | 6 | 0 | 1096,96 |
| 3/4 di Mi♭ | quarta superiore, sesta minore sul Do | La♭≡Sol♯ | 63,281 | 2 | 6 | 4 | 6 | 822,77 |
| 3/2 di Sol♯ | quinta discendente, seconda minore sul Do | Do♯ | 94,922 | 3 | 9 | 6 | 9 | 1234,155 |
| 3/4 di Do♯ | quarta giusta, quarta aumentata sul Do | Fa♯ | 71,191 | 2 | 10 | 2 | 0 | 925,52 |
Una volta trovata l’ottava e suddiviso in dodici semitoni il segmento fra C8′ e c4′, con il compasso si disegna il triangolo equilatero che ha per lato il detto segmento: la base di questo triangolo perciò contiene tutti i tratti corrispondenti ai semitoni. Si congiungono questi ultimi con il vertice opposto. Tracciando un segmento parallelo alla base, passante per le metà dei lati, si ottiene la suddivisione per semitoni della seconda ottava. E nuovamente, tirando un altro segmento parallelo alla base, passante per un quarto dei lati, si individuano le lunghezze delle lastre della terza ottava. Si ripete il procedimento con segmenti paralleli passanti per 1/8, 1/16 e 1/32 dei lati per trovare le ottave più acute.La cosiddetta “correzione di bocca” è una quantità (pari a circa due volte il diametro della canna), che si deve sottrarre dalla lunghezza teorica per approssimarsi a quella reale. Essa è trascurabile in fase di progettazione, ma nel caso di canne molto larghe e acute assume valori rilevanti.
Il sistema geometrico basato sulle coordinate cartesiane consente di analizzare tre parametri, vincolati fra loro da relazioni funzionali ben precise:
- Disponendo le canne in ordine ascendente dal grave all’acuto, si stabilisce una relazione biunivoca fra il numero progressivo di nota e la lunghezza d’onda.
- Nel caso di adozione del sistema pitagorico (o di altri sistemi frazionari) la serie si rappresenta con i valori discreti stabiliti dal sistema stesso per ciascun intervallo all’interno della prima ottava, e con i loro sottomultipli nelle ottave acute secondo le potenze di 2 (nella seconda ottava saranno dimezzati, nella terza saranno ridotti a 1/4, nella quarta a 1/8, e così via).
- Nel caso del sistema equabile moderno la serie è rappresentata con una funzione del tipo y=k/12√2x-1 che si può scrivere anche y=k·2(1-x)/12, in cui la variabile indipendente x è data dal numero d’ordine del tasto, la variabile y è la lunghezza della corrispondente canna e la costante k è stabilita dall’unità di misura della lunghezza stessa. Nel caso dell’unisono x vale 1, l’esponente si annulla, il denominatore equivale all’unità e dunque y risulta determinato dalla sola costante dimensionale k (8′ oppure 2,6 m); nel caso della quarta x vale 6 (numero di tasti che separano le note costituenti l’intervallo, incluso quello da cui s’inizia a contare), l’esponente diventa -5/12 e perciò y si ottiene dividendo k per 12√25.
- Le lunghezze ottenute con i metodi illustrati al punto precedente possono essere usate per determinare le larghezze in funzione del rapporto di lastra, che a sua volta può essere costante o variabile. Ponendo come ascisse le lunghezze e come ordinate le larghezze di canna questa relazione genera sul piano cartesiano un nuovo grafico:
- se tale relazione è di tipo lineare continuo si ottiene appunto una retta,
- se invece è di tipo lineare discontinuo si ottiene una linea spezzata.
Per esigenze di spazio la lunghezza di lastra, o almeno quella delle note più gravi, può essere ridotta in scala: per le proprietà dei triangoli simili il risultato non cambia.
- Le larghezze possono però anche essere stabilite indipendentemente dalle rispettive lunghezze, ad esempio con il dimezzamento delle aree delle sezioni trasversali delle canne in corrispondenza delle ottave, oppure imponendo il dimezzamento del diametro dopo un certo intervallo solitamente maggiore dell’ottava, o ancora fissando un rapporto d’ottava diverso da 1÷2: in tutti questi casi la relazione non è più lineare, e quindi il grafico è curvilineo.
Delle canne labiali: calcolo delle progressioni