Progressioni non lineari
Sino ad ora abbiamo descritto progressioni lineari, i cui grafici mostrano uno o più segmenti consecutivi nel piano cartesiano. In questo contesto la retta è l’ente geometrico che rappresenta la relazione lineare fra lunghezza e larghezza di lastra. Tuttavia la ricerca di timbri e dinamiche condotta da musicisti e costruttori di strumenti musicali portò inevitabilmente a metodi geometrici per il calcolo di progressioni non lineari. L’organaria individuò nuove vie già nel Cinquecento, quando iniziò la costruzione di registri di colore e da concerto, con taglie più larghe di quelle usate nei Principali.
Christhard Mahrenholz, Die Berechnung der Orgelpfeifenmensuren vom Mittelalter bis zur Mitte des 19. Jahrhunderts, Bärenreiter-Verlkag, Kassel, 1968 afferma a pagina 40 di trovare tale criterio esplicitato graficamente addirittura in un manoscritto borgognone della seconda metà del Quattrocento. La progressione seguita a questo scopo prevedeva il dimezzamento dei valori della larghezza di lastra non già di ottava in ottava, ma ogni due ottave, ossia nell’intervallo di XV. Però la serie aveva la particolarità di non essere lineare, cioè non può essere rappresentata con segmenti di retta, infatti il rapporto fra le larghezze di lastra di due canne distanti un intervallo d’ottava è fatto pari a 1 ÷ 2√2.
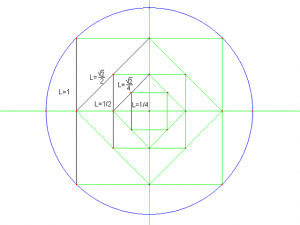
Per suddividere geometricamente l’ottava in semitoni si può sfruttare il teorema di Pitagora, costruendo il triangolo rettangolo che ha una cateto pari alla larghezza di lastra della canna acuta e l’altro cateto pari alla metà della larghezza di lastra della canna grave: l’ipotenusa è pari alla larghezza di lastra della canna acuta moltiplicata per √3/2. Questa nuova misura dà la larghezza della quinta pura (che poco si discosta da quella della quinta temperata). Sfruttando il circolo delle quinte e moltiplicando per √2 i valori che eccedono l’ottava si ricostruisce la successione dei dodici semitoni.
Una progressione così concepita porta a canne gravi relativamente strette e a canne acute molto larghe, avvicinandosi, per così dire, ai più rigidi modelli medievali in cui i diametri erano mantenuti pressoché costanti attraverso un’estensione di poche ottave.
Per suddividere geometricamente l’ottava in semitoni si può sfruttare il teorema di Pitagora, costruendo il triangolo rettangolo che ha una cateto pari alla larghezza di lastra della canna acuta e l’altro cateto pari alla metà della larghezza di lastra della canna grave: l’ipotenusa è pari alla larghezza di lastra della canna acuta moltiplicata per √3/2. Questa nuova misura dà la larghezza della quinta pura (che poco si discosta da quella della quinta temperata). Sfruttando il circolo delle quinte e moltiplicando per √2 i valori che eccedono l’ottava si ricostruisce la successione dei dodici semitoni.
Una progressione così concepita porta a canne gravi relativamente strette e a canne acute molto larghe, avvicinandosi, per così dire, ai più rigidi modelli medievali in cui i diametri erano mantenuti pressoché costanti attraverso un’estensione di poche ottave.
Non deve sorprendere l’uso di numeri irrazionali, giacché, come s’è detto, il metodo geometrico permette di risolvere le operazioni di calcolo agevolmente: in un quadrato il lato e la diagonale sono appunto in rapporto di 1:√2. Per i teoremi di Euclide in un triangolo rettangolo, l’altezza relativa all’ipotenusa è medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa e dunque si può costruire il triangolo in cui sussista la relazione 1 ÷ √2 = √2 ÷ 2
Dal punto di vista dei teorici che il Mahrenholz cita, de Caus e Mersenne, questa progressione poteva essere usata in registri tappati o per un Principale aperto di 16′.
Dal punto di vista dei teorici che il Mahrenholz cita, de Caus e Mersenne, questa progressione poteva essere usata in registri tappati o per un Principale aperto di 16′.
Si possono inoltre sfruttare le proprietà geometriche dei poligoni regolari, in cui i lati e le diagonali hanno precisi rapporti: nel pentagono è nota la relazione aurea di 1 a (√5+1)/2 (equivalente approssimativamente a 1:1,618); nell’esagono vale il rapporto 1 a √3 (approssimato a 1:1,732). Inoltre si possono costruire triangoli rettangoli i cui cateti sono in proporzione con l’ipotenusa secondo valori irrazionali che non si scostano molto da quello individuato in epoca moderna da Töpfer con la citata Normalmensur 1:4√8 (circa 1:1,682). Per esempio se i cateti misurano 3 e 4 l’ipotenusa vale 5, e quindi si stabiliscono esplicitamente le note relazioni 3:5 (circa 1:1,6667) e 4:5; oppure se i cateti valgono 1 e 2 l’ipotenusa è √5, e così via.

Durante i secoli XVII e XVIII la letteratura teorica in lingua tedesca comincia a trattare espressamente scale in cui le larghezze di lastra rispettano i seguenti rapporti d’ottava 4:7, 5:9, 3:5, 5:8, 5:7, 2:3. In particolare sappiamo che doveva essere piuttosto diffusa l’adozione del rapporto 3:5 nei registri ad anima e del rapporto 5:7 in quelli ad ancia. La tabella qui sotto permette di riconoscere lo sviluppo di diverse progressioni, aventi in comune tutte lo stesso valore per il Do di 2′.
| · | 1÷2 | 5÷9 · 1÷1,8 |
4÷7 · 1÷1,75 |
7÷12 · 1÷1,714 |
3÷5 · 1÷1,667 |
sectio aurea 1÷1,618 |
5÷8 · 1÷1,6 |
2÷3 · 1÷1,5 |
1÷√2 · 1÷1,414 |
5÷7 · 1÷1,4 |
3÷4 · 1÷1,333 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C8′ | 200 | 162 | 153 | 147 | 139 | 131 | 128 | 113 | 100 | 98 | 89 |
| C4′ | 100 | 90 | 87,5 | 85,7 | 83,3 | 80,9 | 80 | 75 | 70,7 | 70 | 66,7 |
| C2′ | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| C1′ | 25 | 27,8 | 28,6 | 29,2 | 30 | 30,9 | 31,3 | 33,3 | 35,4 | 35,7 | 37,5 |
| C½’ | 12,5 | 15,4 | 16,4 | 17,0 | 18 | 19,1 | 19,6 | 22,2 | 25 | 25,5 | 28,1 |
Delle canne labiali: calcolo delle progressioni