Dom Bédos versus Töpfer
Axel Leuthold in un articolo citato rimarca più volte il fatto che Mahrenholz erroneamente calcola i diametri delle canne mediante equazioni esponenziali, mentre i valori che gli Antichi ottenevano derivano da più semplici equazioni lineari. Questo errore non è affatto trascurabile. Per le ascisse, cioè per le lunghezze di lastra, calcolare la successione dei semitoni con il metodo delle proporzioni pitagoriche o con l’estrazione di radice porta a differenze non molto rilevanti dal punto di vista pratico. Invece se le ordinate non sono stabilite in funzione della lunghezza, ma con il criterio logaritmico i risultati sono completamente diversi.
Per chiarire meglio il concetto seguirò prima il ragionamento di Dom Bédos e poi quello di Töpfer.
Per chiarire meglio il concetto seguirò prima il ragionamento di Dom Bédos e poi quello di Töpfer.
Dom Bédos traccia i due assi cartesiani, sulle ascisse riporta la suddivisione pitagorica, quindi stabilisce la larghezza di lastra col giusto rapporto di misura in corrispondenza della prima canna grave (Do1 = 155,7 mm), analogamente fissa quella dell’ultima canna acuta (Do49 = 21,4 mm), e disegna poi la linea retta che congiunge i due punti, ricavando sull’asse delle ordinate le larghezze di lastra delle note intermedie.
Secondo il metodo di Töpfer invece, si stabilisce prima il rapporto che deve intercorrere fra le due larghezze di lastra e poi si suddivide questo rapporto nel numero di semitoni compresi; perciò, applicando questo ragionamento ai valori posti da Dom Bedos, si ha 48√(155,7÷21,4)=1,0422112. Questa è la ragione costante fra ciascun semitono: il Do♯2 si ricava da 155,7/1,0422112=149,4, il Re3 da 149,4/1,0422112=143,3, e così via, come illustrato nella tabella seguente.
| Equabile | Dom Bédos | Töpfer | Differenza | ||
|---|---|---|---|---|---|
| 1 | C | 155,7 | 155,7 | 155,7 | 0 |
| 2 | C♯ | 147,7 | 148,4 | 149,4 | 1 |
| 3 | D | 140,1 | 139,8 | 143,3 | 3,5 |
| 4 | D♯ | 132,9 | 133,3 | 137,5 | 4,2 |
| 5 | E | 126,1 | 125,6 | 132 | 6,4 |
| 6 | F | 119,8 | 119,9 | 126,6 | 6,7 |
| 7 | F♯ | 113,7 | 114,4 | 121,5 | 7,1 |
| 8 | G | 108,1 | 107,9 | 116,6 | 8,7 |
| 9 | G♯ | 102,7 | 103,1 | 111,9 | 8,8 |
| 10 | A | 97,6 | 97,3 | 107,3 | 10 |
| 11 | A♯ | 92,8 | 93 | 103 | 10 |
| 12 | B | 88,3 | 87,9 | 98,8 | 10,9 |
| 13 | C | 84,1 | 84,1 | 94,8 | 10,7 |
| 14 | C# | 80,1 | 80,4 | 91 | 10,6 |
| 15 | D | 76,3 | 76,1 | 87,3 | 11,2 |
| 16 | D♯ | 72,7 | 72,9 | 83,7 | 10,8 |
| 17 | E | 69,3 | 69 | 80,4 | 11,4 |
| 18 | F | 66,1 | 66,2 | 77,1 | 10,9 |
| 19 | F♯ | 63,1 | 63,4 | 74 | 10,6 |
| 20 | G | 60,3 | 60,2 | 71 | 10,8 |
| 21 | G♯ | 57,6 | 57,8 | 68,1 | 10,3 |
| 22 | A | 55 | 54,9 | 65,3 | 10,4 |
| 23 | A♯ | 52,6 | 52,7 | 62,7 | 10 |
| 24 | B | 50,4 | 50,2 | 60,2 | 10 |
| 25 | C | 48,3 | 48,3 | 57,7 | 9,4 |
| 26 | C♯ | 46,2 | 46,4 | 55,4 | 9 |
| 27 | D | 44,4 | 44,3 | 53,1 | 8,8 |
| 28 | D♯ | 42,6 | 42,7 | 51 | 8,3 |
| 29 | E | 40,9 | 40,7 | 48,9 | 8,2 |
| 30 | F | 39,3 | 39,3 | 46,9 | 7,6 |
| 31 | F♯ | 37,8 | 37,9 | 45 | 7,1 |
| 32 | G | 36,3 | 36,3 | 43,2 | 6,9 |
| 33 | G♯ | 35 | 35,1 | 41,5 | 6,4 |
| 34 | A | 33,7 | 33,7 | 39,8 | 6,1 |
| 35 | A♯ | 32,5 | 32,6 | 38,2 | 5,6 |
| 36 | B | 31,4 | 31,3 | 36,6 | 5,3 |
| 37 | C | 30,4 | 30,4 | 35,1 | 4,7 |
| 38 | C♯ | 29,3 | 29,4 | 33,7 | 4,3 |
| 39 | D | 28,4 | 28,4 | 32,4 | 4 |
| 40 | D♯ | 27,5 | 27,6 | 31 | 3,4 |
| 41 | E | 26,7 | 26,6 | 29,8 | 3,2 |
| 42 | F | 25,9 | 25,9 | 28,6 | 2,7 |
| 43 | F♯ | 25,1 | 25,2 | 27,4 | 2,2 |
| 44 | G | 24,4 | 24,4 | 26,3 | 1,9 |
| 45 | G♯ | 23,7 | 23,8 | 25,2 | 1,4 |
| 46 | A | 23,1 | 23,1 | 24,2 | 1,1 |
| 47 | A♯ | 22,5 | 22,5 | 23,2 | 0,7 |
| 48 | B | 21,9 | 21,9 | 22,3 | 0,4 |
| 49 | C | 21,4 | 21,4 | 21,4 | 0 |
Nella colonna a sinistra sono riportati i diametri risultanti dalla suddivisione dell’ottava secondo il sistema equabile, nella colonna centrale quelli ricavati dal metodo grafico di Dom Bédos e in quella a destra i dati forniti dal calcolo di Töpfer, con a fianco le differenze: si nota che esse raggiungono addirittura il centimetro. Invece le differenze fra la disposizione delle ascisse con il sistema equabile e quelle con il pitagorico sono di poco conto. Riportate in grafico, le progressioni dei due autori appaiono decisamente non sovrapponibili.
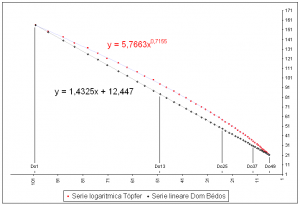
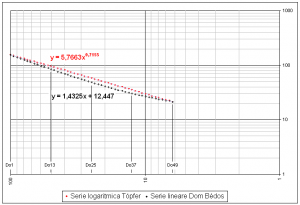
Come si nota nel primo grafico, l’andamento delle larghezze è lineare nel caso della scala di Dom Bédos e curvilineo (funzione di potenza) in quella di Töpfer. Se però scegliamo di distribuire le ordinate e le ascisse logaritmicamente allora possiamo rappresentare la scala di Töpfer mediante una retta, e di conseguenza quella di Dom Bédos con una curva, come illustrato nel secondo grafico.
Le equazioni evidenziate permettono di ricostruire le progressioni con un normale foglio elettronico. Caratteristica del grafico logaritmico è la distribuzione equispaziata dei semitoni; di conseguenza la distanza fra due note di ugual nome è sempre la stessa: fra Do1 e Do13 c’è lo stesso spazio che troviamo fra Do13 e Do25 o fra Do25 e Do37 o Do37 e Do49. Invece nel grafico proporzionale l’asse delle ascisse mostra la naturale successione delle ottave secondo le potenze di 2: la distanza fra Do13 e Do25 è la metà di quella fra Do1 e Do13, quella fra Do25 e Do37 è 1/4, fra Do37 e Do49 1/8.
Le equazioni evidenziate permettono di ricostruire le progressioni con un normale foglio elettronico. Caratteristica del grafico logaritmico è la distribuzione equispaziata dei semitoni; di conseguenza la distanza fra due note di ugual nome è sempre la stessa: fra Do1 e Do13 c’è lo stesso spazio che troviamo fra Do13 e Do25 o fra Do25 e Do37 o Do37 e Do49. Invece nel grafico proporzionale l’asse delle ascisse mostra la naturale successione delle ottave secondo le potenze di 2: la distanza fra Do13 e Do25 è la metà di quella fra Do1 e Do13, quella fra Do25 e Do37 è 1/4, fra Do37 e Do49 1/8.
Delle canne labiali: calcolo delle progressioni